MaximaのGnuplotによるグラフ作成
MaximaのGnuplotによる3次元グラフ(媒介変数)
Maxima(マキシマ)でGnuplotを使い、媒介関数の3次元グラフを作成する方法について説明します。
plot3d( [ x(s,t), y(s,t), z(s,t) ],
演算
Maxima
媒介変数の3次元グラフ
では実際にMaximaを使って、媒介変数の3次元グラフを作成してみましょう。

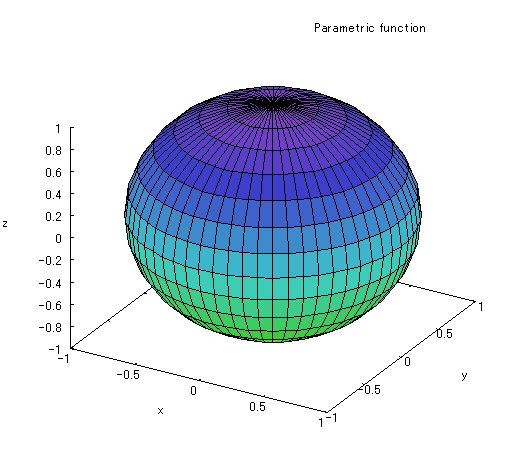
1つ目の式![]() をGnuplotでグラフ化してみると、きちんと球になっているのが分かります。
をGnuplotでグラフ化してみると、きちんと球になっているのが分かります。
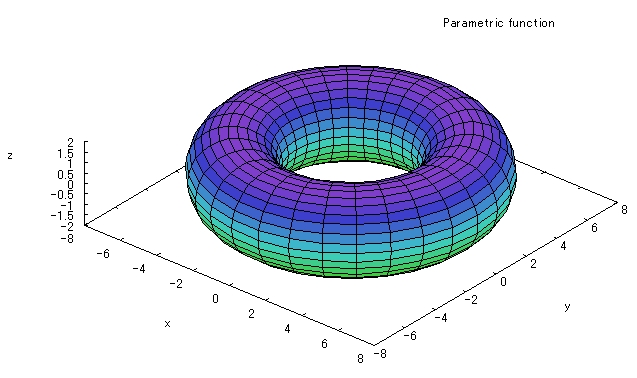
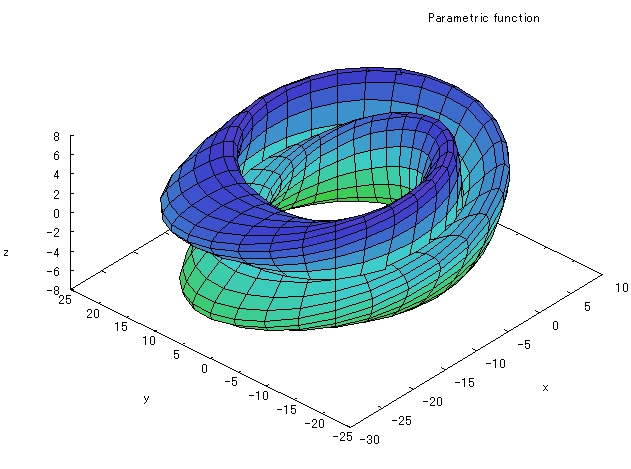
2つ目の式![]() は、ドーナツ型のトーラスです。
は、ドーナツ型のトーラスです。
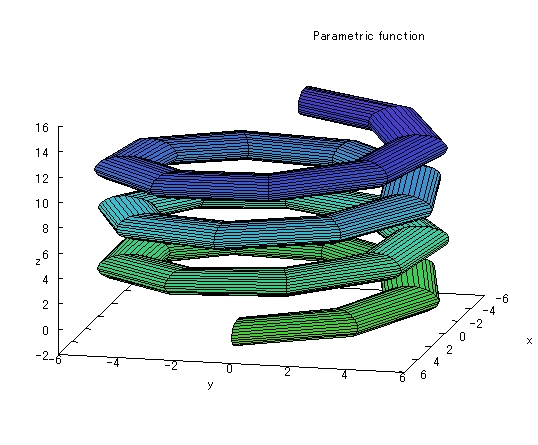
3つ目の式![]() は、バネ型の3次元グラフで、当HPサイトのトップページにアニメーションにしたものです。
は、バネ型の3次元グラフで、当HPサイトのトップページにアニメーションにしたものです。
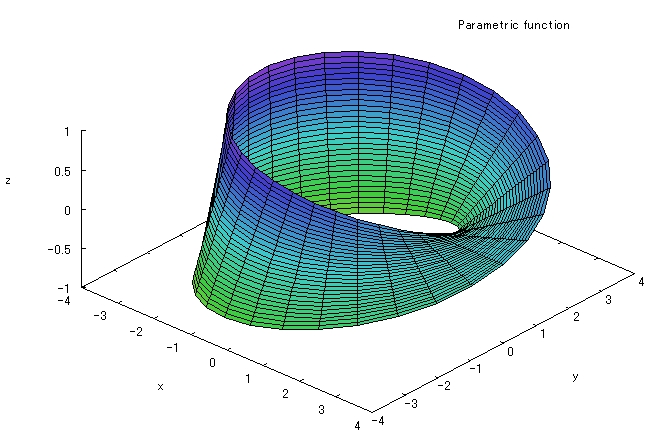
4つ目の式![]() は、メビウスの帯(メビウスの輪)として有名なグラフで、長方形の帯を180度くるっとまわして、端と端をくっつけた形状のものです。
は、メビウスの帯(メビウスの輪)として有名なグラフで、長方形の帯を180度くるっとまわして、端と端をくっつけた形状のものです。
5つ目の式は、次の3式からなるクラインの壺です。
![]()
![]()
![]()
位相幾何学で扱われる形状で、ドイツの数学者フェリックス・クラインが考案したことから、その名がついています。
このように、大変興味深い形状のグラフも難なく表示してくれますので、たくさんトライしてみるのも楽しいです。
