Maximaによる数式処理 Maximaの逆三角関数、双曲線関数
数式処理ソフトMaxima(マキシマ)での逆三角関数を紹介します。
逆三角関数の演算
Maxima
sin()の逆関数
asin()
cos()の逆関数
acos()
tan()の逆関数
atan()
sec()の逆関数
asec()
csc()の逆関数
acsc()
cota()の逆関数
acot()
逆三角関数とは、三角関数の逆関数のことです。
sin(サイン)、cos(コサイン)、tan(タンジェント)のそれぞれの逆三角関数(逆関数)は、マキシマではasin、acos、atanとなります。
同様に、sec(セカント)、csc(コセカント)、cot(コタンジェント)のそれぞれの逆三角関数(逆関数)は、マキシマではasec、acsc、acotです。
注意が必要なのは、逆三角関数は逆関数であり、逆数ではありません。
![]()
![]()
![]()
マキシマでの逆三角関数の使用例を示します。


きちんと逆関数になっていることが確かめられました。
| 逆三角関数の演算 | Maxima |
| 平方根 | sqrt() |
| 絶対値 | abs() |
なお、式中にでてきたsqrt()は平方根で、abs()は絶対値のことです。
次に、指数関数からなり、三角関数と同様に加法定理が成立する双曲線関数を示します。
| 演算 | Maxima |
| 双曲線正弦関数 | sinh() |
| 双曲線余弦関数 | cosh() |
| 双曲線正接関数 | tanh() |
なお、双曲線正弦関数、双曲線余弦関数、双曲線正接関数は、下記であらわされる関数のことです。
![]()
実際に、Maximaを使ってみましょう。
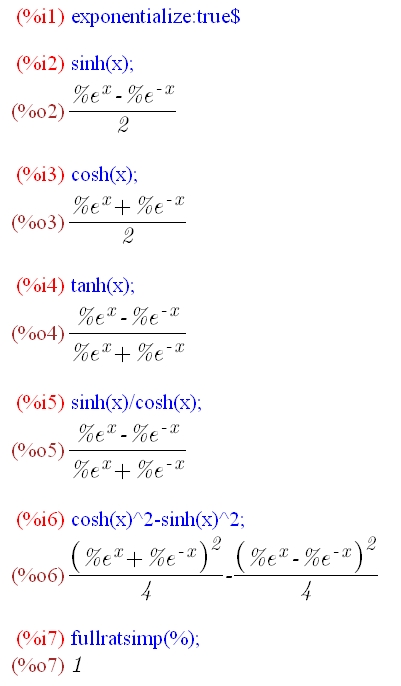
このことから、双曲線正弦関数と双曲線余弦関数の次式の関係も導けました。
![]()
なお、ここで用いたexponetializeは指数関数表示で、fullratsimp()は式をできるだけ簡略化する関数です。
演算
Maxima
指数関数表示
exponentialize:ture
式の簡略化
fullratsimp()
