Maximaによる数式処理 Maximaの微分積分
数式処理ソフトMaxima（マキシマ）での微分積分を紹介します。
まず、微分の基となる極限ですが、マキシマでは極限値はlimit()で求めます。
極限の演算子を示します。
演算
Maxima
極限値
limit( 関数f(x), 変数x, 近づける値a, 近づける方向（plus,minus))
極限値limit（ 関数f(x), 変数x, 近づける値a, 近づける方向（plus,minus,省略）で、
を与えます。
なお、近づける方向は、＋（プラス）方向か、－（マイナス）方向、または省略することができます。
１つ目の式は、自然対数の底eの定義の式です。
３つ目の極限値は、プラス方向から０に近づけた極限値で、
一方、４つ目の極限値は、マイナス方向から０に近づけた極限値です。
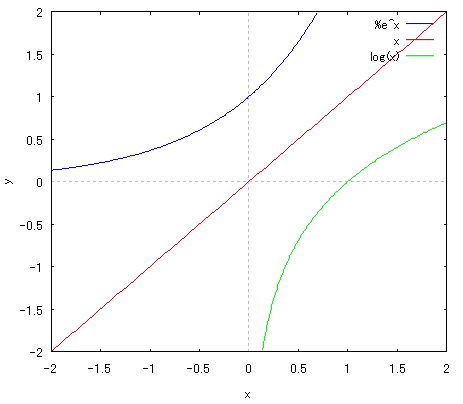
Maximaで数学の微分積分を解くのに、ここでは次のようなグラフで考えてみます。
関数
の
に対して対象となる逆関数の
の微分積分を扱います。
マキシマの微分演算子を示します。
| 演算 | Maxima |
| 微分 |
diff( 関数f(x), 変数x, 変数xの微分回数, 変数y, 変数yの微分回数,…) |
では、対数関数を微分してみます。
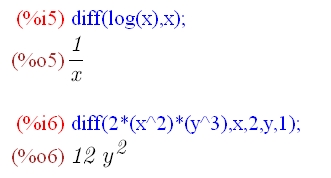
次に、Maximaの微分演算子を示します。
| 演算 | Maxima |
| 不定積分 |
integrate( 関数f(x), 変数x） |
| 定積分 | integrate( 関数f(x), 変数x, 定数aから, 定数bまで） |
対数関数を積分してみましょう。
８つ目の式
から、定義域[1,2]のとx軸で囲まれた面積が求まりました。
では、検算もかねて、区分求積法で同じ値が求まるかを確かめてみます。
対数関数の定義域[1,2]で区分求積法を用いると、数列和の収束
を求めることになります。
実際に、Maximaでこの式を解いてみます。
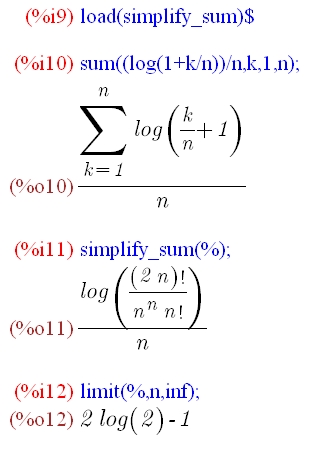
数列和の収束を求めるのに、まず数列和を１０個目の式で計算していますが、得られた出力は式そのもので、計算はされていません。
そこで、１１個目の式で、simpfliy_sum()を用いて実際に計算させています。
最後に、１２個目の式で、nを無限大にして収束する値を求めました。
この値は、８個目で計算した値と同じになっていますので、区分求積法でも同じ値が得られることが確かめられました。
なお、Maximaで、数列和の収束を求めたいときには、simplify_sumパッケージをロードしておきます。
| 演算 | Maxima |
| 数列和の収束演算パッケージをロード | load(simplify_sum)$ |
| 数列和 | sum( 数列関数f(n), 項目変数n, 初値a, 終値b) |
これで、よく使われる等差数列や等比数列などをはじめ数列の和の収束を計算してくれます。